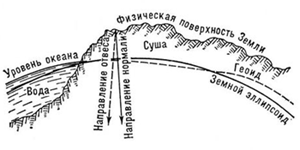
Уклонения отвесных линий (отклонение отвеса)

В общем случае поверхность геоида и поверхность эллипсоида не параллельны между собой. Вследствие этого ввели понятие об уклонениях отвесных линий.

Уклонение отвесной линии (отклонение отвеса) — угол u образованный при несовпадении отвесной линии проведенной в точке на земной поверхности перпендикулярно геоиду с проведенной в этой же точке перпендикулярно к эллипсоиду нормалью.

Уклонением отвесной линии от нормали к общеземному эллипсоиду называется абсолютным, а от нормали к референц-эллипсоиду  — относительным.

Если уклонение отвесной линии измеряется в плоскости в которой лежат отвесная линия и нормаль к поверхности референц-эллипсоида, то оно называется полным. Обычно полное уклонение отвесной линии. разлагается на две его составляющие равные его проекциям на плоскость меридиана — так называется отклонение в меридиане (по широте) и на плоскость, перпендикулярную к ней — отклонение в первом вертикале, или отклонение по долготе.

Уклонение отвесных линий u в любой точке для практических целей обычно рассматривают не целиком, а в проекции на плоскость меридиана x и на плоскость 1-го вертикала h.

Составляющие уклонений отвесных линий в меридиане x и первом вертикале h определяют путем сравнения астрономической широты f и долготы l точки земной поверхности с её геодезической широтой В и долготой L, причём они выражаются формулами:

x = f – В,
h = (l — L) cosf

Составляющая уклонений отвесных линий в первом вертикале может быть определена также путём сравнения астрономического азимута a и некоторого направления с его геодезическим азимутом А по формуле h = (a — A) ctg f).

Алфавитный указатель

Недавно мне скинули сайт, где было найдено очень много групповушки.